1.01 Unit Checkpoint Triangle Similarity
one.two: Similar Triangles
- Folio ID
- 112401
Congruent Triangles
Two triangles are coinciding if they have exactly the same size and shape. This means that their corresponding angles are equal, and their respective sides accept the aforementioned lengths, every bit shown beneath.

The ii triangles below are congruent. List the corresponding parts, and find the angles \(\theta\), \(\phi\), and \(\chi\), and side \(z\).
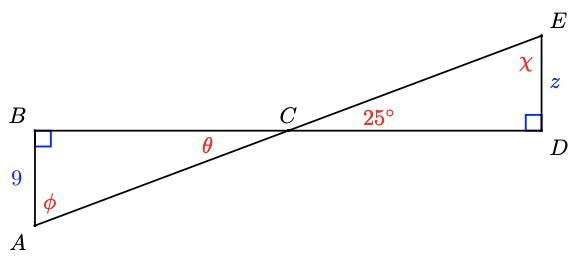
- Answer
-
In these triangles, \(\angle B=\bending D\) because they are both right angles, and \(\bending B C A= \angle D C East\) considering they are vertical angles, and so \(\theta=25^{\circ}\). The third angles, \(\bending A\) and \(\angle E\), must likewise be equal, so \(\phi=\chi=65^{\circ}\). (Practise you come across why?) The sides opposite each pair of corresponding angles are equal, so \(A B=D Due east, B C=C D\) and \(A C=C Eastward\). In particular, nosotros find that \(z=9\).
The two triangles at right are congruent. Observe the values of \(\blastoff, \beta\), and \(\gamma\).

- Answer
-
\( \alpha=85^{\circ}, \beta=75^{\circ}, \gamma=85^{\circ}\)
Recall that the altitude of a triangle is the segment from 1 vertex of the triangle perpendicular to the reverse side.
Bear witness that the altitude of an equilateral triangle divides it into two coinciding correct triangles.
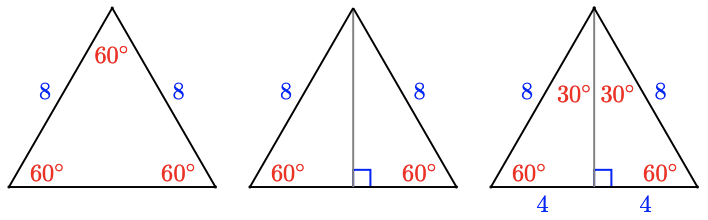
- Answer
-
Consider for example an equilateral triangle of side 8 inches, as shown above. The altitude is perpendicular to the base, so each half of the original triangle is a right triangle. Because each correct triangle contains a \(lx^{\circ}\) bending, the remaining angle in each triangle must exist \(ninety^{\circ}-sixty^{\circ}=30^{\circ}\). Both triangles have a side of length eight between the angles of \(30^{\circ}\) and \(60^{\circ}\), so they are coinciding. (Consequently, the brusk sides of the congruent triangles are equal, so each is half the original base.)
The triangles in the previous example are a special type of right triangle called \(xxx^{\circ}-60^{\circ}-ninety^{\circ}\) triangles. Notice that in these triangles, the leg opposite the \(30^{\circ}\) angle is half the length of the hypotenuse.
The diagonal of a parallelogram divides information technology into 2 congruent triangles, as shown at right. List the respective parts of the two triangles, and explain why each pair is equal.
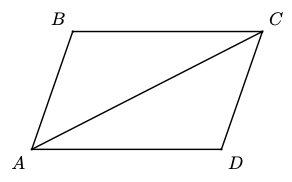
- Answer
-
\(\angle B C A=\angle C A D\) and \(\angle B A C=\angle A C D\) considering they are alternate interior angles. If two pairs of angles in a triangle are equal, so is the third pair, so \(\angle B=\angle D\). \(B C=A D\) and \(A B=C D\) because they are reverse sides of a parallelogram, and \(A C=A C\).
Similar Triangles
Two triangles are similar if they have the same shape but not necessarily the same size. The respective angles are equal, and the corresponding sides are proportional. Nosotros can recollect of one similar triangle as an enlargement or a reduction of the other. (See the figures below.)
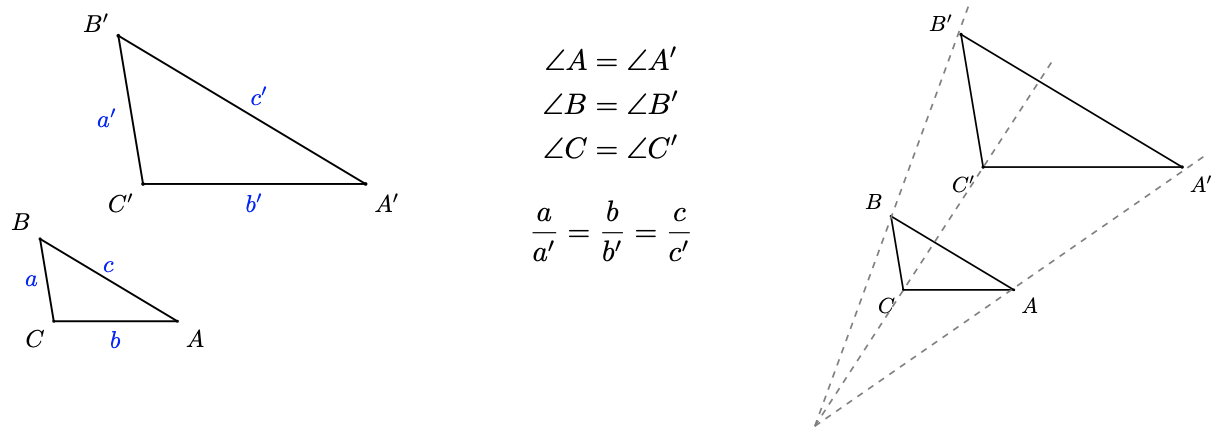
To determine whether two triangles are like, it turns out that we demand to verify simply one of the two conditions for similarity, and the other condition will be true automatically.
Two triangles are similar if either
- their corresponding angles are equal, or
- their corresponding sides are proportional.
Which of the pairs of triangles shown below are similar?
a.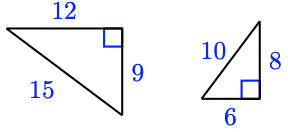
b.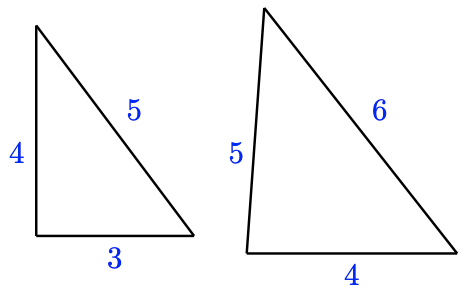
c.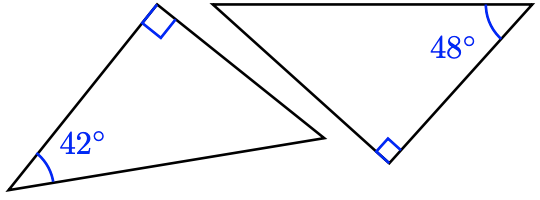
- Answer
-
a. Nosotros volition check whether the corresponding sides are proportional. We compute the ratios of the corresponding sides, making certain to write each ratio in the same order, \(\frac{\text { larger triangle }}{\text { smaller triangle }}\). (The other order, \(\frac{\text { smaller triangle }}{\text { larger triangle }}\), would also piece of work, as long every bit we use the same club for all the ratios.)
shorter legs: \(\dfrac{9}{6} \quad\) longer legs: \(\dfrac{12}{8} \quad\) hypotenuses: \(\dfrac{fifteen}{10}\)
Because all of these ratios are equal to 1.5, the triangles are similar.
b. The ratios of respective sides are not equal: the ratio of the longest sides is \(\frac{6}{5}\), simply the ratio of the smallest sides is \(\frac{four}{3}\). The triangles are not similar.
c. The missing angle of the first right triangle is \(48^{\circ}\), and the missing angle in the 2nd right triangle is \(42^{\circ}\), then three pairs of angles lucifer. The triangles are similar.
Are the triangles below similar? Explain why or why not in each case.
a.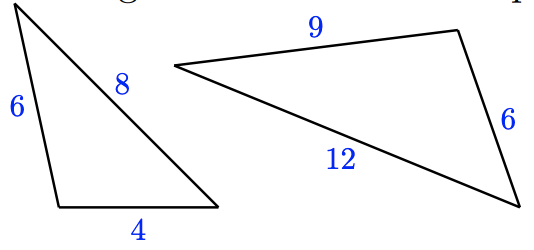
b.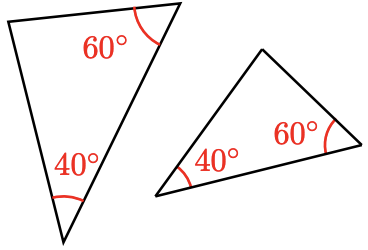
- Respond
-
a. The triangles are similar because \(\frac{iv}{6} = \frac{6}{ix} = \frac{8}{12}\), and then the sides are proportional.
b. The tertiary bending in both triangles is \(eighty^{\circ}\), so the triangles are similar considering their corresponding angles are equal.
Note ane.23 In part (b) of the previous exercise, note that the tertiary angle in each triangle must be \(80^{\circ}\), because the sum of the angles is \(180^{\circ}\). Thus, nosotros demand only bear witness that two pairs of angles are equal to prove that two triangles are like.
Using Proportions with Like Triangles
The figure in the next example shows a parallelogram \(A B C D\) and two triangles, \(\triangle A B E\) and \(\triangle F C East\). Tin nosotros observe the unknown lengths \(ten\) and \(y\) in the larger triangle?
Offset note that two pairs of corresponding angles in the triangles are equal: \(\bending B E A\) and \(\angle F East C\) are vertical angles, and \(\angle East F C\) and \(\angle B A E\) are alternate interior angles. But if two pairs of corresponding angles are equal, then the tertiary pair must be equal also. This means that the two triangles are similar, and nosotros can use the fact that their corresponding sides are proportional to detect \(x\) and \(y\).
Detect the value of \(10\) in the figure at right.

- Answer
-
Nosotros run across that \(ten\) is the length of the shortest side in \(\triangle A B Due east\). We know the short side in \(\triangle F C E\) and the lengths of the medium sides in each triangle. If we form the ratios of the short sides and the medium sides, nosotros obtain the following proportion.
\[\dfrac{\text { larger triangle }}{\text { smaller triangle }}: \dfrac{x}{iv}=\dfrac{fifteen}{6} \nonumber\]
To solve the proportion, we cantankerous-multiply to get
\begin{aligned}
6 x &=4(15)=60 \quad \quad \quad \quad \text{Divide both sides by half dozen.} \\
x &=\dfrac{60}{6}=10
\end{aligned}
Remember that "cantankerous-multiplying" is a brusque-cut technique for solving proportions. It does not work for other operations involving fractions.
Find the value of \(y\) in the previous example.
- Answer
-
\(y=20\)
Similar Right Triangles
If two correct triangles take one pair of respective acute angles with the same measure, then the triangles are similar. Nosotros can utilize this fact most right triangles to make indirect measurements.
Delbert would similar to know the height of a sure building. He gets Francine to concur up a 5-foot pole about the building and measures the length of its shadow. The shadow of the pole is 3 anxiety long, and the shadow of the building is 12 feet long.
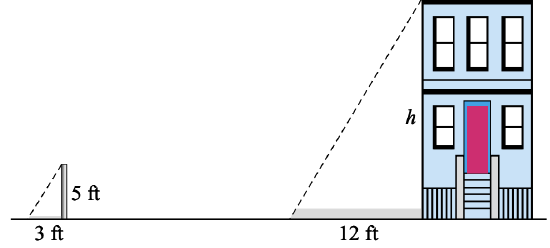
a. Use similar triangles to write a proportion involving the elevation of the edifice.
b. Solve the proportion to find the height of the building.
- Answer
-
a. In the figure above nosotros see two right triangles: One triangle is formed past the edifice and its shadow, and the other past the pole and its shadow. Because the low-cal rays from the sun are parallel, the two angles at the tips of the shadows are equal. Thus, the two right triangles are like, and their corresponding sides are proportional. The ratios of heights and bases in the two triangles yield the proportion
\[\dfrac{\text{larger triangle}}{\text{smaller triangle}}: \dfrac{h}{5} = \dfrac{12}{three}\]
b. To solve the proportion, nosotros cross-multiply to get
\begin{aligned}
3h& = 5(12) = lx \quad \quad \quad \quad \text{Carve up both sides past 3.} \\
h&=\dfrac{lx}{three} = 20
\end{aligned}The building is 20 feet tall.
Earlier we created a \(30°-60°-90°\) triangle in which the shorter leg was four inches and the hypotenuse was 8 inches. The hypotenuse of another \(xxx°-threescore°-90°\) triangle is five feet. What is the length of the side reverse the \(30°\) angle?
- Answer
-
\(2.5\) feet
Overlapping Triangles
In some applications, similar triangles may share a side or an angle.
Place two similar triangles in the effigy at right, and write a proportion to find \(H\).
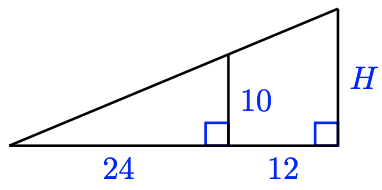
- Answer
-
The two triangles overlap, sharing the marked bending, as shown beneath. Because each triangle likewise has a right angle, they are like.
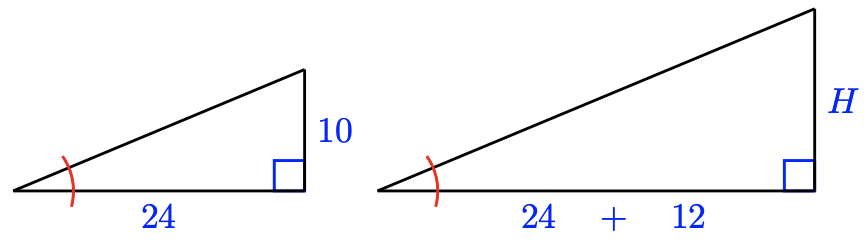
Note that the base of the larger triangle is \(24 + 12 = 36\). The ratio of the heights and the ratio of the bases must exist equal, so we write the following proportion.
\brainstorm{aligned}
\dfrac{H}{x} &= \dfrac{36}{24} \quad \quad \quad \quad &&\text{Cross-multiply.} \\
24H &= 360 &&\text{Carve up both sides by 24.} \\
H &= \dfrac{360}{24} = 15
\end{aligned}
Heather wants to know the height of a street lamp. She discovers that when she is 12 feet from the lamp, her shadow is 6 feet long. Find the acme of the street lamp.
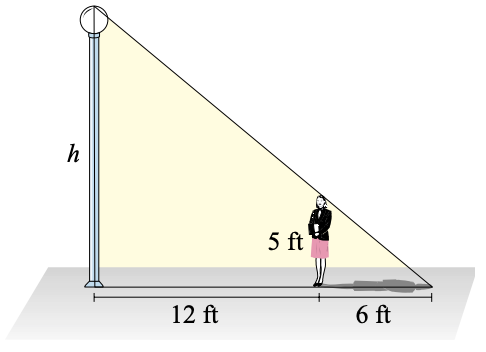
- Reply
-
\(xv\) feet
Review the post-obit skills you will need for this department.
Which of the post-obit expressions and equations are proportions?
1. \(\dfrac{7}{x} = \dfrac{3}{5}\)
two. \(\dfrac{10}{2} = \dfrac{eight}{10+2}\)
3. \(1+\dfrac{x}{4} = \dfrac{2x}{three}\)
iv. \(\dfrac{6}{x} + \dfrac{x}{5}\)
5. \(\dfrac{3}{x+ane} \cdot \dfrac{2x}{v}\)
half-dozen. \(\dfrac{one}{x} + \dfrac{2}{3x} = \dfrac{x-2}{2}\)
Solve each equation. Brainstorm by writing an equivalent equation without fractions: multiply both sides past the LCD.
seven. \(\dfrac{x}{12} = \dfrac{3}{ten}\)
eight. \(1+\dfrac{x}{2} = \dfrac{2x}{5}\)
- Algebra Refresher Answers
-
But 1 and 2 are proportions.
vii. \(\pm6\)
8. \(-10\)
Section 1.2 Summary
Vocabulary
Expect upward the definitions of new terms in the Glossary.
• Coinciding
• Altitude
• Leg
• Hypotenuse
• Parallelogram
• Similar
• Proportional
Concepts
1. Two triangles are coinciding if they have exactly the same size and shape.
2. The altitude of an equilateral triangle divides it into two congruent right triangles.
3. In a \(thirty^{\circ}-60^{\circ}-xc^{\circ}\) right triangle, the leg opposite the \(30^{\circ}\) angle is one-half the length of the hypotenuse.
4. Two triangles are like if they have the same shape only non necessarily the same size. The respective angles are equal, and the respective sides are proportional.
5. Two triangles are similar if either
- their corresponding angles are equal, or
- their respective sides are proportional.
6. If two right triangles have one pair of corresponding acute angles with the same measure, then the triangles are like.
Study Questions
1 What is the difference between congruent triangles and like triangles?
ii What is the name of the brusque-cut method for solving proportions? Why does the method work?
three In two triangles, if two corresponding pairs of angles are equal, are the triangles like? How do you lot know?
4 For the triangles shown, which of the following equations is true? Explain why.
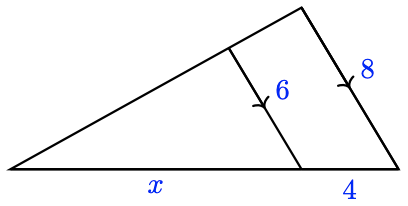
a. \(\dfrac{iv}{x} = \dfrac{6}{8}\)
b. \(\dfrac{x}{4} = \dfrac{6}{eight}\)
c. \(\dfrac{10}{10+four} = \dfrac{half dozen}{8}\)
d. \(\dfrac{x}{x+4} = \dfrac{6}{14}\)
Skills
Practice each skill in the Homework Issues listed.
ane Identify coinciding triangles and notice unknown parts #1-half-dozen
2 Identify similar triangles #vii-10
iii Observe unknown parts of similar triangles #eleven-twenty
4 Solve bug using proportions and similar triangles #21-26
5 Use proportions to chronicle sides of similar triangles #27-38
Homework 1.2
In Problems i–4, proper name two congruent triangles and detect the unknown quantities.
1. \(P QRS\) is an isosceles trapezoid.

ii.
3. \(\Delta PRU\) is isosceles.
iv. \(\Delta P RU\) is isosceles and \(OR = NG\). Observe \(\angle RNG\) and \(\angle RNO\).
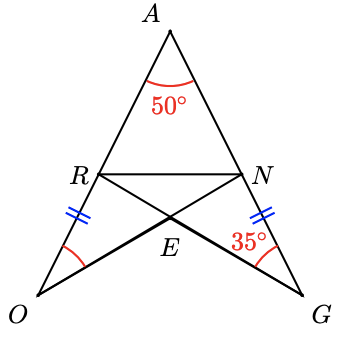
5. Delbert and Francine want to measure the distance across a stream. They mark point \(A\) direct beyond the stream from a tree at point \(T\) on the opposite bank. Delbert walks from point \(A\) downwardly the bank a brusque distance to point \(B\) and sights the tree. He measures the angle between his line of sight and the streambank.
a Draw a figure showing the stream, the tree, and right triangle \(ABT\).
b Meanwhile Francine, who was still standing at point \(A\), walks away from the stream at right-angles to Delbert'south path. Delbert watches her progress, and tells her to stop at point \(C\) when the bending between the stream bank and his line of sight to Francine is the same equally the angle from the stream banking company to the tree. Add triangle \(ABC\) to your effigy.
c Delbert now measures the distance from point \(A\) to Francine at point \(C\). Explain why this altitude is the aforementioned as the distance across the stream.
six. If yous have a baseball cap, here is some other manner to measure the distance across a river. Stand at point \(A\) directly across the river from a convenient landmark, say a big rock, on the other side. Tilt your head downwards and so that the brim of the cap points directly at the base of the stone, \(R\).
a Depict a effigy showing the river, the rock, and right triangle \(ABR\), where \(B\) is the location of your baseball cap on your head.
b Now, without changing the angle of your caput, rotate \(ninety^{\circ}\) and sight along the bank on your side of the river. Have a friend mark the spot \(C\) on the basis where the skirt of your cap points. Add triangle \(ABC\) to your effigy.
c Finally, you lot can measure the distance from point \(A\) to signal \(C\). Explicate why this altitude is the same every bit the distance across the river.
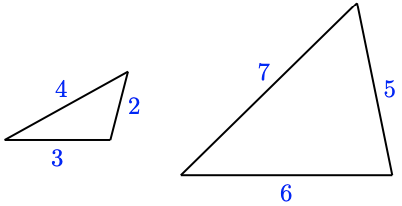
For Bug 7–10, decide whether the triangles are similar, and explain why or why not.
seven.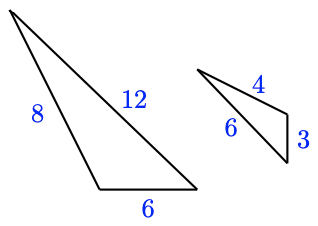
8.
ix.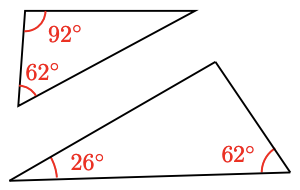
x.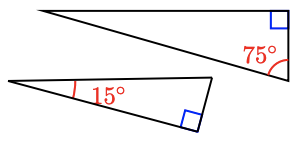
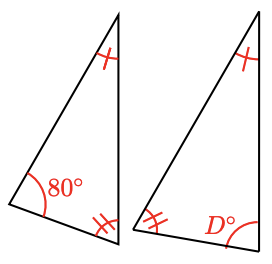
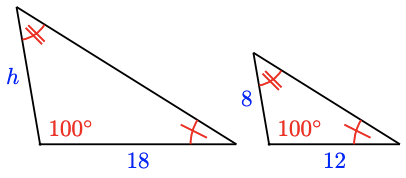
Presume the triangles in Issues eleven–14 are like. Solve for the variables. (Figures are non drawn to scale.)
eleven.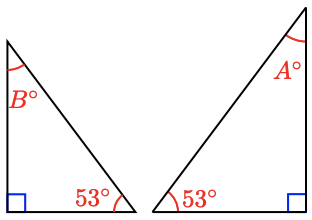
12.
13.
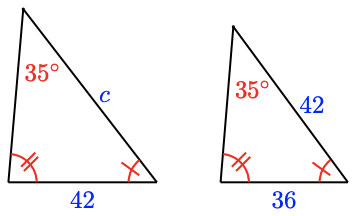
14.
In Problems 15–20, use properties of similar triangles to solve for the variable.
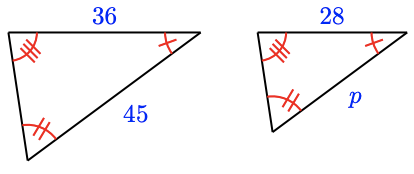
15.
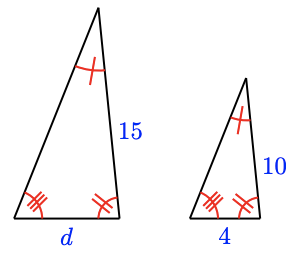
16.
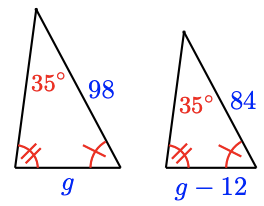
17.
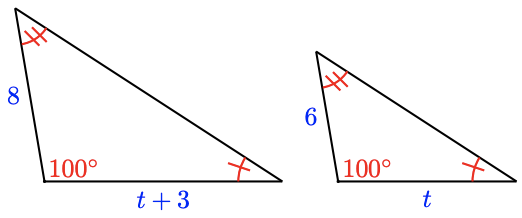
18.
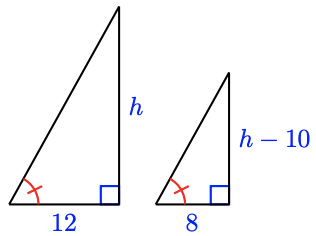
19.
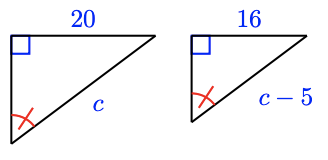
20.
For Problems 21–26, use properties of like triangles to solve.
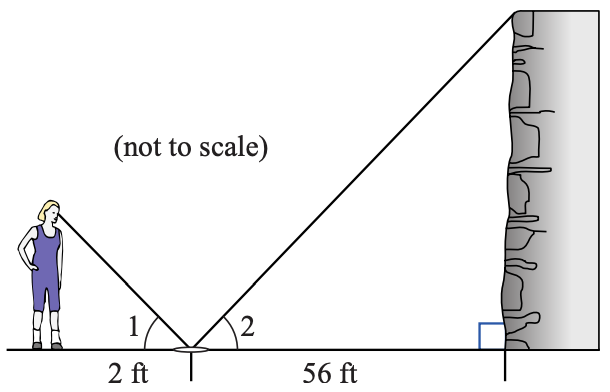
21. A rock climber estimates the summit of a cliff she plans to scale as follows. She places a mirror on the footing so that she can simply see the top of the cliff in the mirror while she stands straight. The angles 1 and 2 formed by the low-cal rays are equal, as shown in the figure. She so measures the distance to the mirror (two feet) and the distance from the mirror to the base of operations of the cliff (56 feet). If she is 5 anxiety 6 inches tall, how high is the cliff?
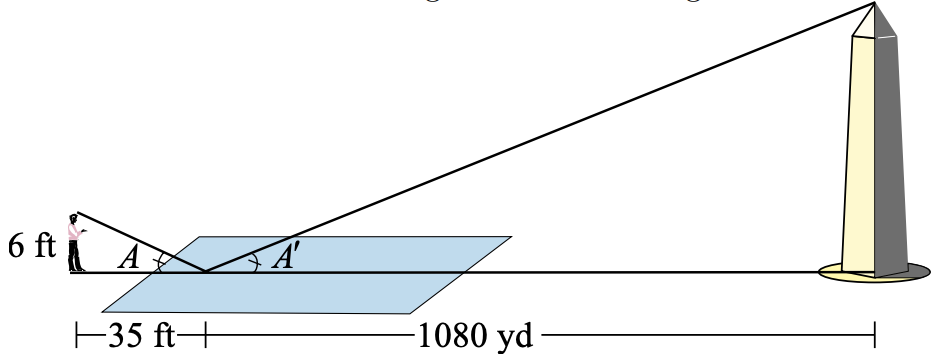
22. Edo estimates the elevation of the Washington Monument as follows. He notices that he tin see the reflection of the meridian of the monument in the reflecting pool. He is feet from the tip of the reflection, and that point is 1080 yards from the base of operations of the monument, as shown below. From his physics grade Edo knows that the angles marked and are equal. If Edo is vi feet tall, what is his gauge for the height of the Washington Monument?
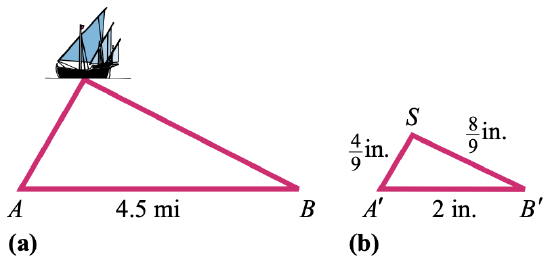
23. In the 6th century BC, the Greek philosopher and mathematician Thales used similar triangles to measure the altitude to a ship at body of water. Two observers on the shore at points \(A\) and \(B\) would sight the ship and measure out the angles formed, equally shown in effigy (a). They would then construct a similar triangle equally shown in figure (b), with the same angles at \(A\) and \(B\), and measure its sides. (This method is called triangulation.) Employ the lengths given in the figures to find the distance from observer to the ship.
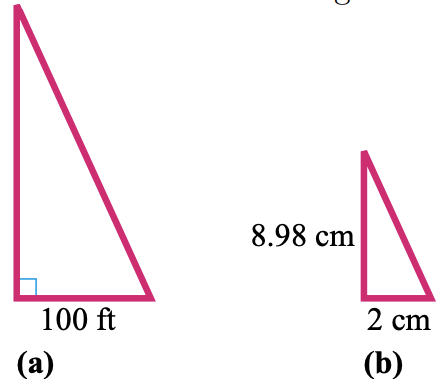
24. The Capilano Intermission Bridge is a footbridge that spans a 230-human foot gorge n of Vancouver, British Columbia. Before crossing the span, y'all decide to estimate its length. You walk 100 anxiety downstream from the bridge and sight its far end, noting the bending formed by your line of sight, every bit shown in figure (a). You then construct a like right triangle with a 2-centimeter base of operations, equally shown in figure (b). You find that the height of your triangle is 8.98 centimeters. How long is the Capilano Suspension Bridge?
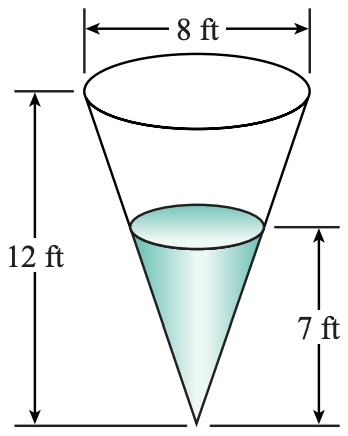
25. A conical tank is 12 feet deep and the diameter of the top is 8 feet. If the tank is filled with h2o to a depth of 7 feet equally shown in the effigy at correct, what is the area of the exposed surface of the h2o?
26. To mensurate the altitude \(EC\) across the lake shown in the effigy at correct, stand up at \(A\) and sight betoken \(C\) across the lake, then mark point \(B\). And so sight to point \(Eastward\) and mark point \(D\) so that \(DB\) is parallel to \(EC\). If \(AD = 25\) yards, \(AE = 60\) yards, and \(BD = 30\) yards, how wide is the lake?

In Issues 27–28, the pairs of triangles are similar. Solve for \(y\) in terms of \(ten\). (The figures are non fatigued to scale.)
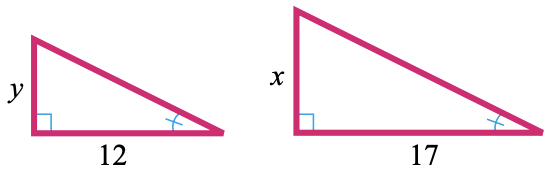
27.
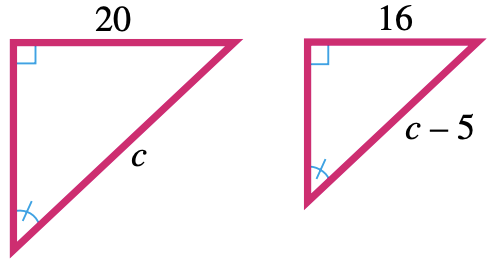
28.
For Issues 29–34, employ properties of like triangles to solve for the variable.
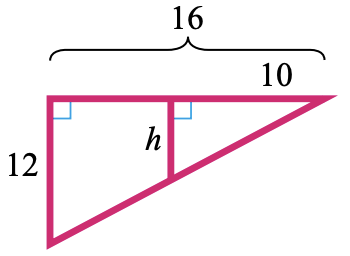
29.
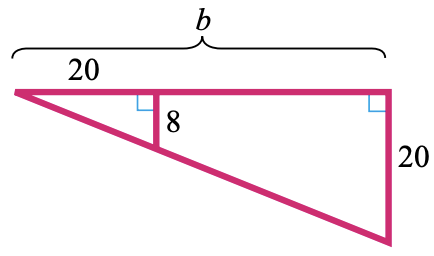
30.
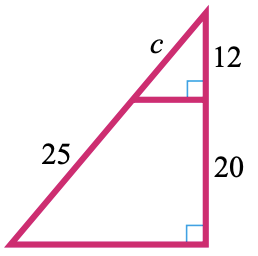
31.
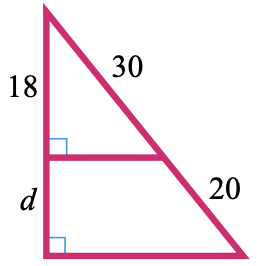
32.
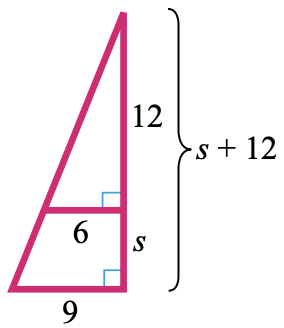
33.
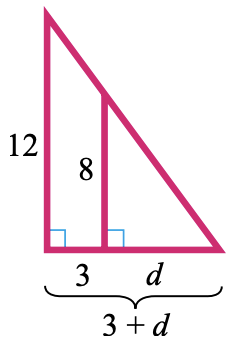
34.
In Problems 35–38, solve for \(y\) in terms of \(ten\)
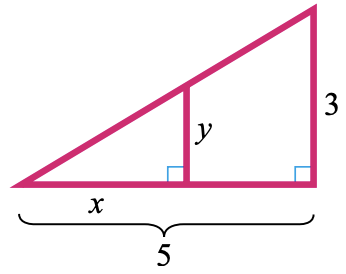
35.
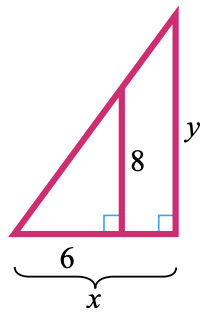
36.
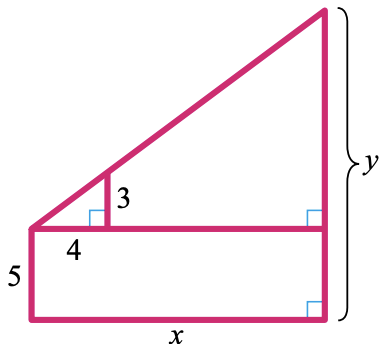
37.
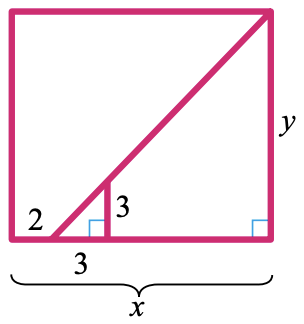
38.
39. Triangle \(ABC\) is a right triangle, and \(Advertizement\) meets the hypotenuse \(BC\) at a right bending.
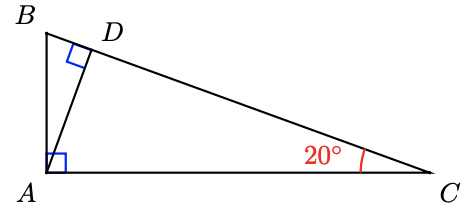
a If \(\angle ACB = twenty^{\circ}\) , find \(\bending B, \angle CAD\), and \(\bending DAB\).
b Find 2 triangles similar to \(\Delta ABC\). List the respective sides in each of the triangles.
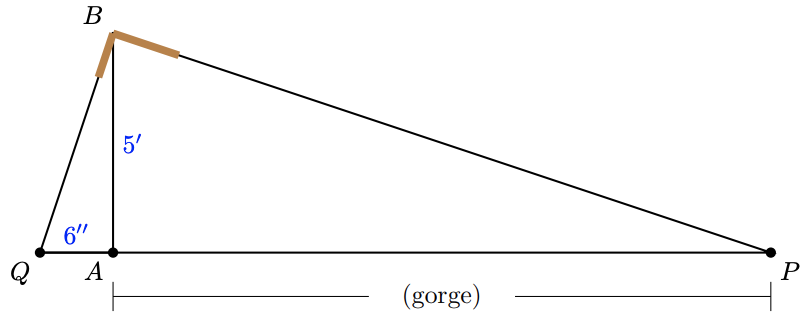
twoscore. Hither is a way to find the distance across a gorge using a carpenter's foursquare and a five-foot pole. Plant the pole vertically on one side of the gorge at point \(A\) and place the angle of the carpenter's square on meridian of the pole at signal \(B\), equally shown in the figure. Sight forth one side of the square and then that it points to the opposite side of the gorge at point \(P\). Without moving the square, sight along the other side and mark point \(Q\). If the distance from \(Q\) to \(A\) is half-dozen inches, calculate the width of the gorge. Explain your method.
1.01 Unit Checkpoint Triangle Similarity,
Source: https://math.libretexts.org/Under_Construction/Trigonometry_(Yoshiwara)/01%3A_Triangles_and_Circles/1.02%3A_Similar_Triangles
Posted by: tuckeramento94.blogspot.com


0 Response to "1.01 Unit Checkpoint Triangle Similarity"
Post a Comment